數據挖掘與應用案例與研討（使用WEKA)

應用案例

台新銀行：應用數據挖掘，提升成案率與效益，行銷案(單件效益從970萬 ~ 1376萬)
應用既有房貸顧客基礎，建置房貸顧客進件違約風險預測模型
中華航空：高艙等促銷模型建置（提升高艙等的座艙率）
財稅局：快速找出虛設行號的營業人

關於資料挖掘

可以預測行銷回應率，不過，主管想知道的是建立模型的效益，是否能幫公司賺錢
資料挖掘＝領域知識＋資料分析（人力＋資料）
數據可說明關係，因果要透過人為分析
有機驗的領域專家，能找出重要參數或衍生性參數(e.g. 貸款預測將性別與婚姻混合考慮)
先要求多些資料，後續清除與CODING時再篩選，也能避免模型重要因子曝光
資料前處理的重要性與花費時間位居首位，有高品質的數據，才有高品質的數據挖掘結果
透過Cross-Validation 將樣本透過不同抽樣樣本，找出最佳的預測結果
區隔化模型：將客戶分群，針對不同客戶群，找出適合的變數與模型

資源分享

Kdnuggets: Data Mining 必知網站, Gregory Piatetsky Shapiro
Kaggle, 公司提供資料辦分析比賽有獎金
解讀大數據,公視

什麼是數據挖掘?

數據挖掘 Data Mining
定義
- 從現有的⼤量數據中，擷取不明顯、之前未知、可能有用的知識,William Frawley & Gregory Piatetsky Shapiro, 1991
目標
- 建⽴決策模型，哪一類的使⽤者對我的產品有興趣?
- 根據過去的⾏行動來預測未來的⾏為

數據挖掘工具

WEKA is a collection of machine learning algorithms for data mining tasks. The algorithms can either be applied directly to a dataset or called from your own Java code.
- Download and install WEKA, support Windows x32/x64 and Mac OS X
R is a free software environment for statistical computing and graphics.

知識探勘步驟

資料選擇: 找出與問題相關的資訊
資料清理: 問題資料處理(typo,missing,資料一致性）
- 類神經、邏輯回歸，不允許資料內有空值
- 透過 Mean +/- 3 Std，超出範圍判定為離群值
資料擴充: 連結其他資訊來源擴充其他資訊
資料編碼:
- 將過度詳細的資料編碼
  - 將地址編碼成區域
  - 將生日編碼成年齡
  - 將收入分成幾個級距
  - 將yes/no 編碼成 1/0
- 不同編碼方式，會決定不同的資料模式
- 會重複執行，直到找到較好的結果
- 資料攤平
- 類別數值在8個之內，可以考慮變更為類別屬性
資料挖掘
產出報告

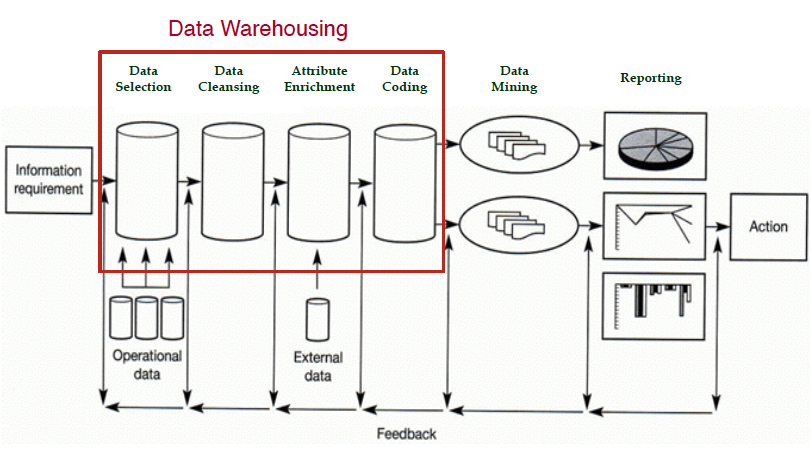
Cross Industry Standard Process- Data Mining, CRISP-DM

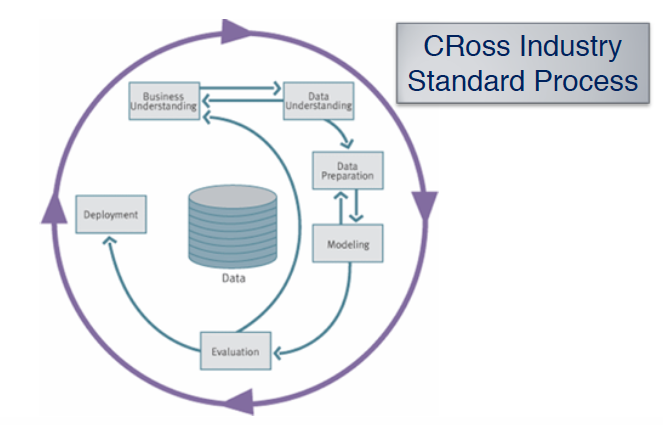
比較CRISP-DM 與KDD
- Business Understanding: Information Requirement
- Data Preparation: Data Selection, Data Cleansing, Attribute Enrichment, Data Coding
- Model: Data Mining
- Evaluation: Reporting
- Deployment: Action

基本資料挖掘技術

Query Tool
Statistical Techniques
Visualization Techniques
Case-Based Learning

Mining Models

描述性(Unsupervised Learning)
- 關聯規則(Association Rules)：事件常常一起出現（Amazon，依據訂單找出關聯性的商品）
- 序列型樣(Sequential Pattern)：事件會循序出現（實體賣場coupon、登山設備、攝影設備、設備更新）
- 聚類分析(Cluster Analysis)：數據間的內部結構
預測性 (Supervised Learning)
- 分類(Classification)：預測數據所隸屬的類別
- 預測(Prediction)：預測數據所對應的數值

預測性資料挖掘

Classification (分類)：目標屬性為類別
- Bayes Net (⾙貝式網路)
- Decision Tree (決策樹)：J48
- Neural Network (類神經網路)
- Logistic Regression (羅吉斯回歸)
- Support Vector Machine(支持向量機)
Prediction (預測)：目標屬性為類別數值
- Linear Regression (線性回歸)
- Decision Tree (決策樹): J48
- Neural Network (類神經網路): Random Forest
- Support Vector Machine(⽀支持向量機)
- Time Series (時間序列)

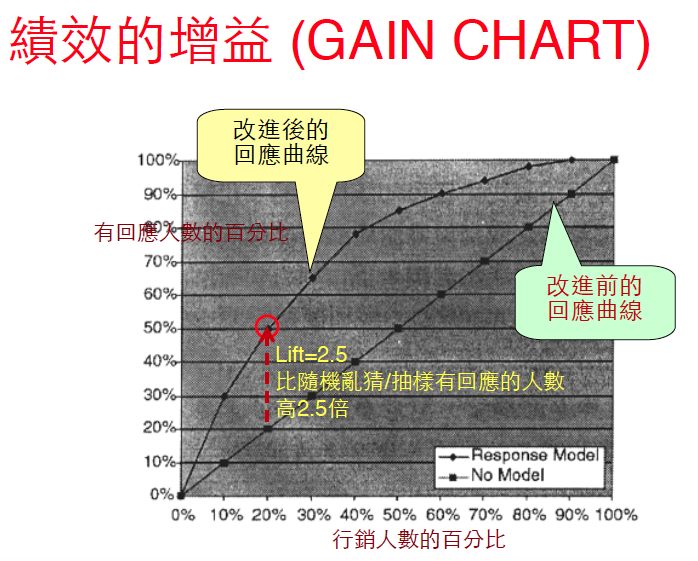
績效的增益

假設
- 促銷總顧客數: 100萬
- 總回應顧客數: 1萬
從顧客中隨機挑選 20% (20萬)的顧客來寄發直效郵件
- 預期回應顧客數: $$10,000 * 20\% = 2000$$
- 預期收益: $$200044–198,0001–20,000=-130,000$$
利⽤用Data Mining來改進Response Rate
- 預期回應顧客數: $$10,000*50\%=5000$$
- 預期收益: $$500044–195,0001–20,000=+5,000$$
顧客數優化: 該寄發給多少顧客?
Gaint Chart:用模型訓練資料後，依照預測機率排序（由大到小）繪製行銷人數與預測結果的關係圖
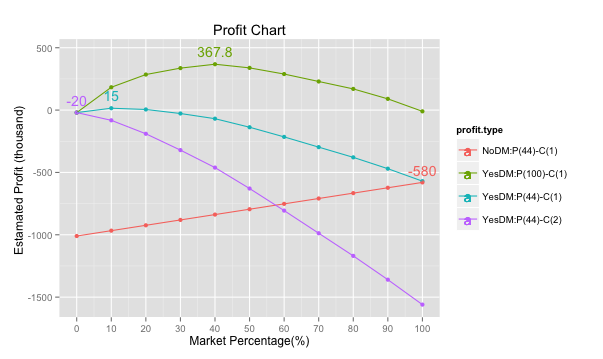
Profit Chart：透過不同行銷比例的收益估算結果，找出收益最高的百分比，不同獲利與成本假設，會造成不同最適百分比

模型

10則交叉驗測
- Cross-Validation是透過10次採樣結果計算平均的正確率，最後的模型是用所有訓練資料去建立模型
Overfitting Problem
- 將模型貼近大量訓練資料(increase train-set accuracy) ，造成模型實際預測性降低(decrease test-set accuracy)

Classify模型

rules
- Zero-R: 依照眾數（類別）/平均值（數值）進行預測，當模型準確率基準
- One-R
  - 視同一層的決策樹
  - 每個屬性值用ZeroR方式計算錯誤率，找出錯誤率最小的屬性
trees > J48：決策數
bayes > Naive Bayes:
lazy > IBK(KNN):
rules > PART

關鍵變數發掘技術

數值型欄位重要性因子，可用T-檢定
- 依照分類計算平均值(Mean)與標準差(Std)
- $$ \frac{|Mean_1 - Mean_2|}{ (Std_1 + Std_2)/2} $$
類別型欄位重要性因子，可用卡方檢定
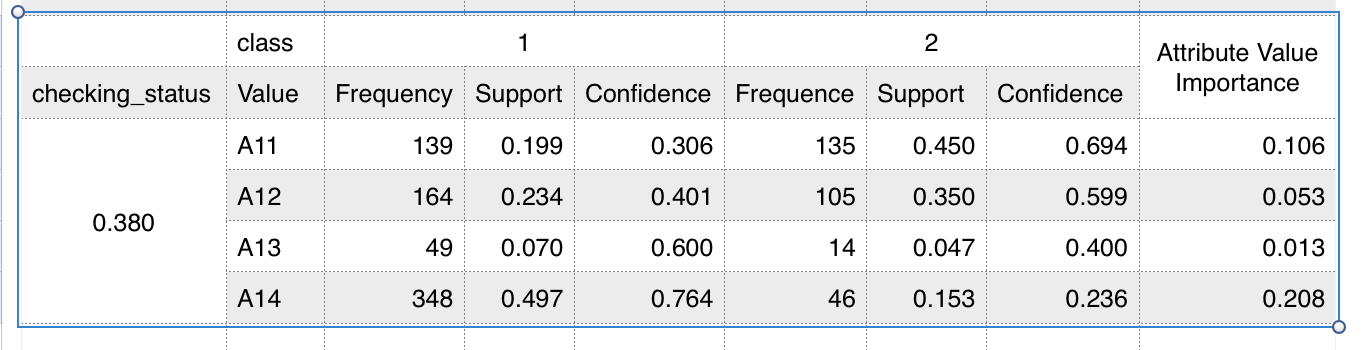
- 分群計算每個數值的個數(Frequency)與百分比(support)
$$ confidence_{A11,1} = \frac{0.199}{(0.199 + 0.450)} = 0.30 $$
$$ importance_{A11} = |0.306 - 0.694| \frac{139+135}{139+164+49+348+135+105+14+46} = 0.106 $$
$$ importance{checking_status} = \sum{i=A11}^{A14} importance_i $$

Naive Bayes

假設每個屬性彼此獨立且重要性相同，依照每個屬性計算機率取大值
漸增式學習，模型訓練容易，資料收集後可丟棄，建立查表，容易大數據應用
避免特定ZeroValue造成機率為零無法區分，透過次數 offset = 1處理
空值處理：測試時忽略該屬性不計算機率
透過決策樹，篩選重要欄位，進行學習可以提升正確率
大多數防毒軟體都是透過貝氏原理進行學習

貝氏分類法 Bayesian Network

評估模型預測結果

目標欄位為類別，透過混亂矩陣 Confusion Matrix
- 實際結果與預測結果的比對表
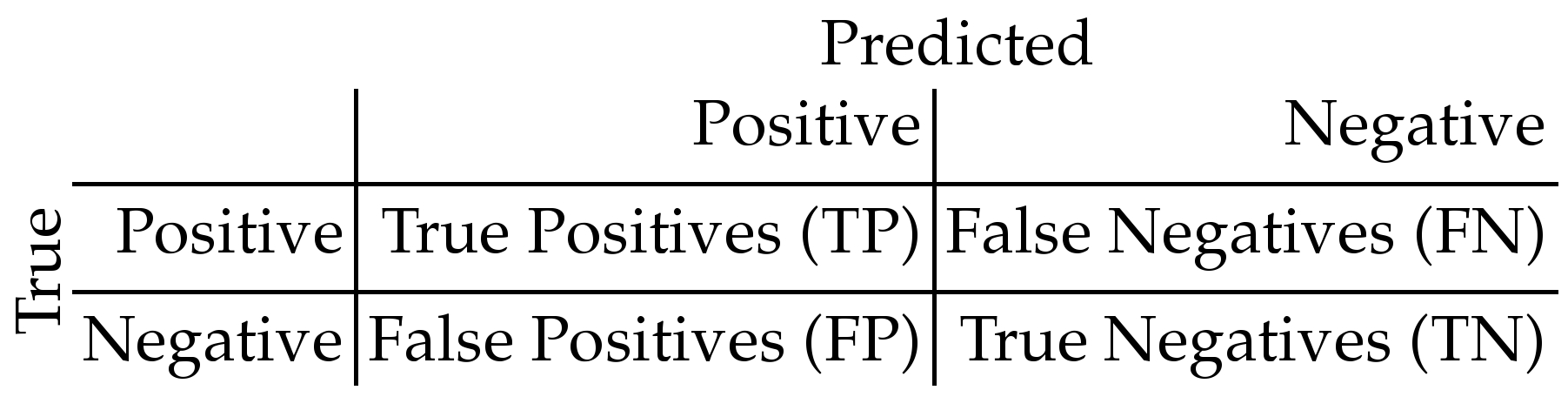
- 命中率 Precision of Positive = $$\frac{TP}{(TP +FP)}$$
- 捕捉率 Recall for Positive = $$\frac{TP}{(TP + FN)}$$
- F指標 F-Index: $$ \frac{ 2 Precision Recall }{ (Precision + Recall)} $$
- 正確率 Accuray = $$ \frac{(TP + TN)}{(TP + FN + FP + TN)} $$
目標欄位為類別，透過預測結果與實際結果的誤差值
- MAE(Mean Absolute Error)
- MSE(Mean Squared Error) = $$\sum_{i=1}^n(Y_i - Y_i)^2 $$
- $$R^2$$

線性回歸

只接受數值欄位
預測客戶年收入，推銷財富管理（單位獲利最高），不過，銀行獲利最大為房貸
如何知道資料源，住址轉區域（郵局）
數值預測相對分類，難度高很多
預測模型好壞
- MAE, Mean Absolute Error
- MSE, Mean Squared Error
- $$ R^2 $$,

決策樹

分類樹：目標欄位為類別
- 知名實作 ID3 > C4.5(J48) > C5.0: Tree generation algorithms, Ross Quinlan (recursive divide-and-conquer)
- 遞迴式依照屬性將資料分群
- 使用正確率最高
- 砍樹（當樹狀分群資料過少，代表性不足）
- ID3: Information Gain
  - 不考慮砍樹，沒考慮噪音處理
  - 節點選擇偏向挑選分類項目多屬性
  - 只能處理類別屬性，數值要透過離散化處理
  - 欄位屬性數據不能有空值
  - 將預測資料直接依照分類樹判斷結果判斷預測結果
  - 將分類樹優化成分類規則，用規則判斷預測資料結果
- C4.5(J48)
  - Gain Ratio = $$\frac{Information Gain}{Information Value} $$
  - 透過Information Value修正數值屬性選項多分數多的情況
  - 透過數值排序後，自動離散化成兩群，找出最佳的切割點（二分法）
  - 空值依據最大正確率的數值填補空值，再進行模型處理
回歸樹(model tree)：目標欄位為數值
- CART:透過屬性分堆計算平均值 (Gini Index)
  - 透過分群計算變異數改變量決定分類樹節點
  - $$ variance = variance_a count_a/count_total + variance_b count_b / count_total $$
  - 數值欄位，透過數值排序後，挑出讓變異數降低最多的切割
- MP:屬性分堆樹再建線性回歸模型
- CHAID: Chi-Square Statistic卡方檢定
- C4.5: Gain Ratio

類神經網路

Input:
- 只接受0~1的數值型資料
  - 數值：透過極值正規化
  - 類別：透過資料攤平展開多個欄位
Output
Hidden Layer
- combinination function $$ Xj = \sum{i=1}^{n} xi * w{ij} + \theta $$
- transfer function(Sigmoid function) $$ V_j = \frac{1}{(1+e^-X_j)} $$
- $$ Error = \sum_{j=1}^{n} T_j - O_j $$
- Neural Network Applet

聚類分析

沒有目標屬性可以分類
依輸入值內容將資料分群
- 相同群組資料要相近，不同群組內容差異要大
- 通常拿數值欄位進行分析，比較少用類別屬性
實作模型
- K-Means：
  - 好處：簡單，計算快速適合大數據使用
  - 壞處：
    - Sensitive to Outliners，會將離群者產生一群
    - 非最佳解，會因為不同開始點有不同分群結果
    - 只能處理數值資料
  - 常用方法
    - 隨機選取Ｋ個沒有缺失值的觀察點
    - 先選擇一個觀察體當第一群的種子，拿超過標準值的點當第二個群的種子
- Kohonen SOM
關心重點
- 數量表示成員間的相似性
  - 直角距離
  - 直線距離
- 依據相似性將成員分群
  - Exclusive v.s. Non-Exclusive (EM)
  - 階層式：
    - 依照距離兩兩群集，依照透過距離將分群到期望數量
    - Single Link：考慮單一資料距離最近
    - Complete Link: 考慮個群集內所有資料的距離最短
  - 分割式
    - 指定要分幾群
- 成員分群完畢後，對每一群的性質進行描述

Reference

R Markdown Example